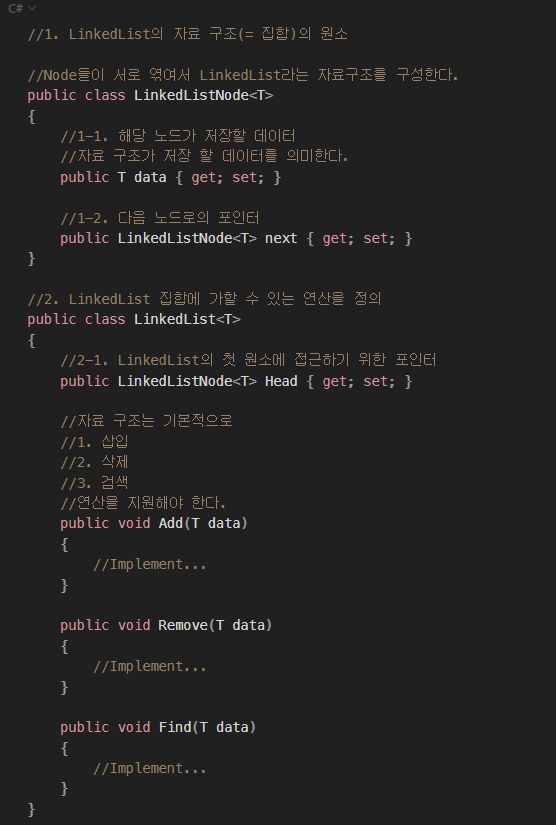
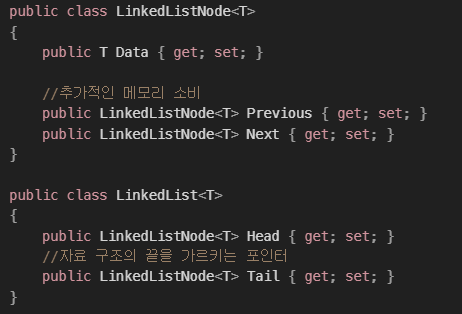
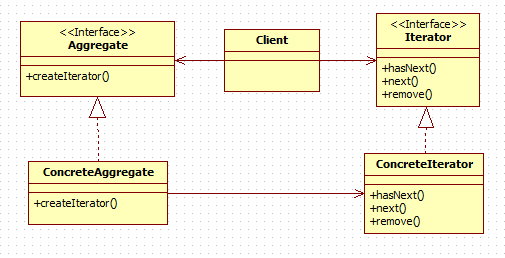
목표 지점까지 최단 경로를 찾아내는 그래프 알고리즘으로, Dijkstra 알고리즘을 그대로 Continuous한 현실 문제에 적용하기 어려웠던 문제를 보안했다.
그리고 h(x)라는 새로운 함수를 추가해서 기존 Dijkstra 보다 더 빠르게 최단 경로를 찾아낸다.
A* Algorithm의 기본적인 형태는 아래와 같다.
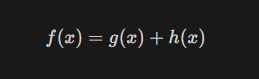
g(x) : 시작 위치에서 “현재 위치 x”까지의 실제 비용
h(x) : “현재 위치 x”에서 부터 “목표 위치”까지의 추정되는 비용
f(x) : 시작 위치에서 “현재 위치 x”까지의 총 추정 비용
따라서, f(x) = g(x)면 Dijkstra와 같다.
알고리즘의 동작은 아래와 같이 진행된다.
- 아직 처리해야하는 노드들 중 가장 작은 f(x) 값을 가지는 노드를 선택한다.
- 이 때 해당 노드가 destination이면 Algorithm을 종료한다.
- 아니라면 방문 했다는 표시를 남기고 현재 노드에서 갈 수 있는 노드들을 본다.
- 현재 노드에서 갈 수 있는 노드들의 가중치 값을 수정한다.
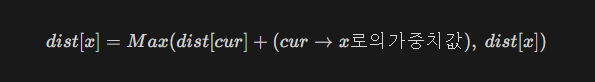
여기 까지는 Dijkstra와 동일 - f(x) = dist[x] + h(x)를 계산한다.
- (f(이웃 노드), 이웃 노드) Pair를 Priority Queue에 저장한다.
- (1)에서 부터 다시 반복한다.
그림으로 알고리즘의 동작을 보자.
아래 그림과 같이 Graph가 있다고 생각하자. 이 때 (1)번에서 시작해서 (7)번까지 최단 경로를 찾는다고 해보자.
Close Set은 최단 경로인지 처리가 완료된 노드들이 들어가는 집합이다. 노드를 중복해서 검사하는 것을 방지
Open Set은 최단 경로를 분석하기 위해 계속해서 노드들이 추가되며, f(x)값이 작은 순서대로 저장된다.
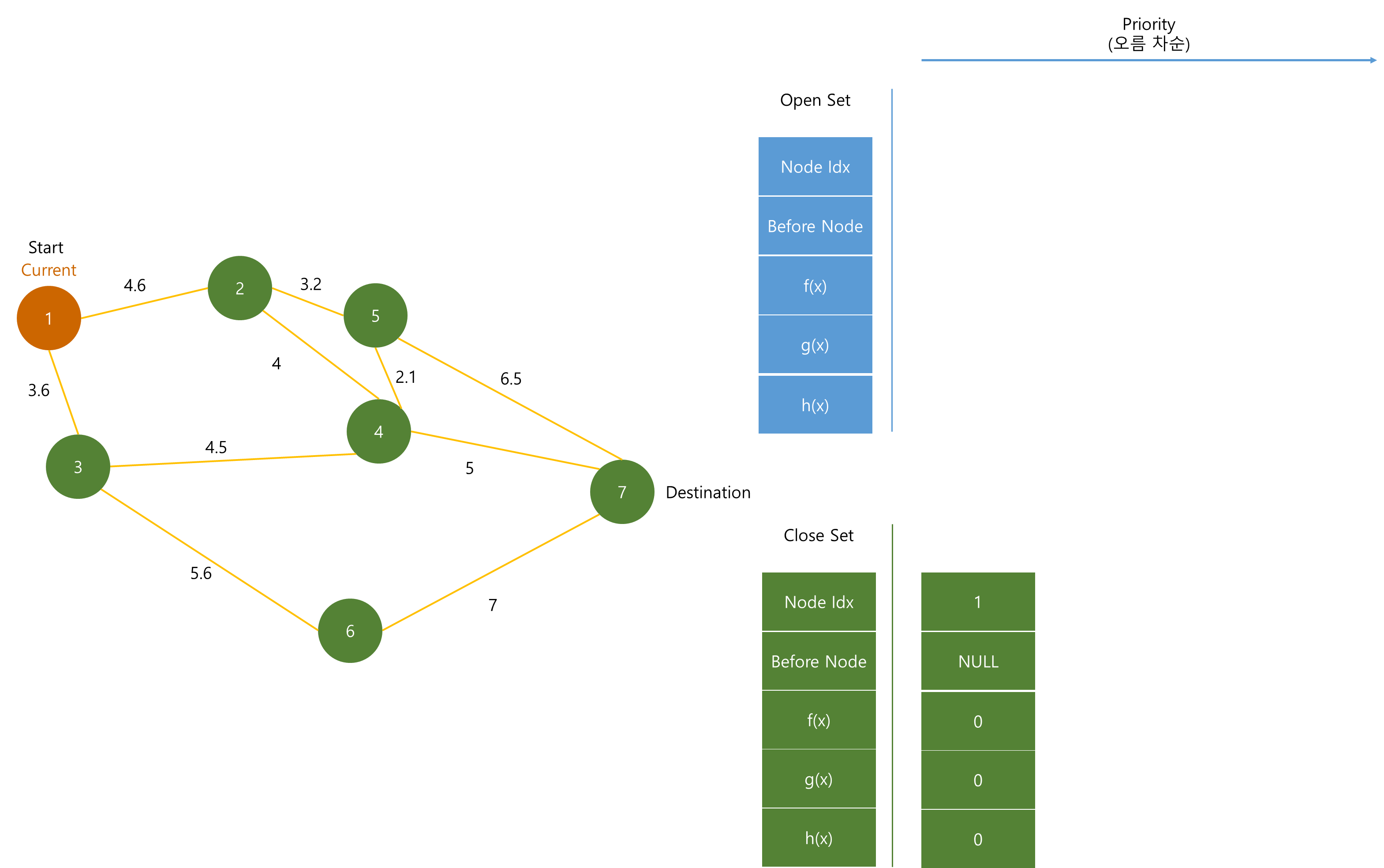
먼저 시작 노드인 (1)을 Close Set에 저장한다.
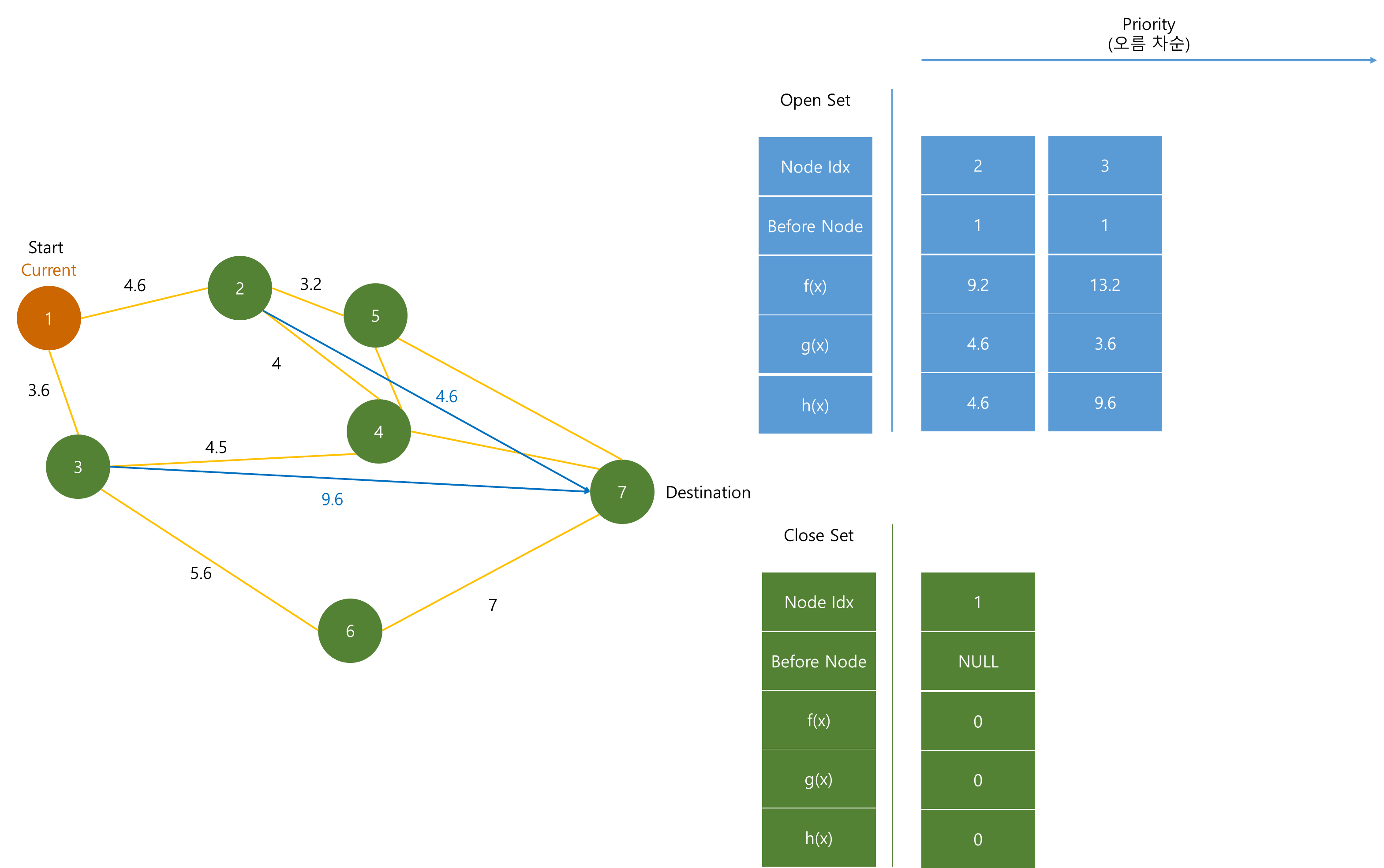
그 후 이웃 노드들 (2), (3)의 dist를 수정하고 (= 그림에서 g(x)) 수정한 값을 h(x)와 더한다.
이 때 h(x)는 해당 노드에서 도착 노드까지의 측정 함수로써 다양한 함수들이 존재하며 알고리즘 성능에 큰 영향을 미친다. 보통은 "맨하탄 거리", "유클리드 거리"를 사용한다. (그림에서는 대략적으로 (2), (3)의 도착지까지의 거리를 각각 4.6, 9.6으로 측정 했다고 가정)
그 후 Priority Queue에 저장한다.

(2), (3) 노드 중 (2)가 f(x)가 작으니 Priority Queue에서 pop 된 후 Close Set에 저장된다.
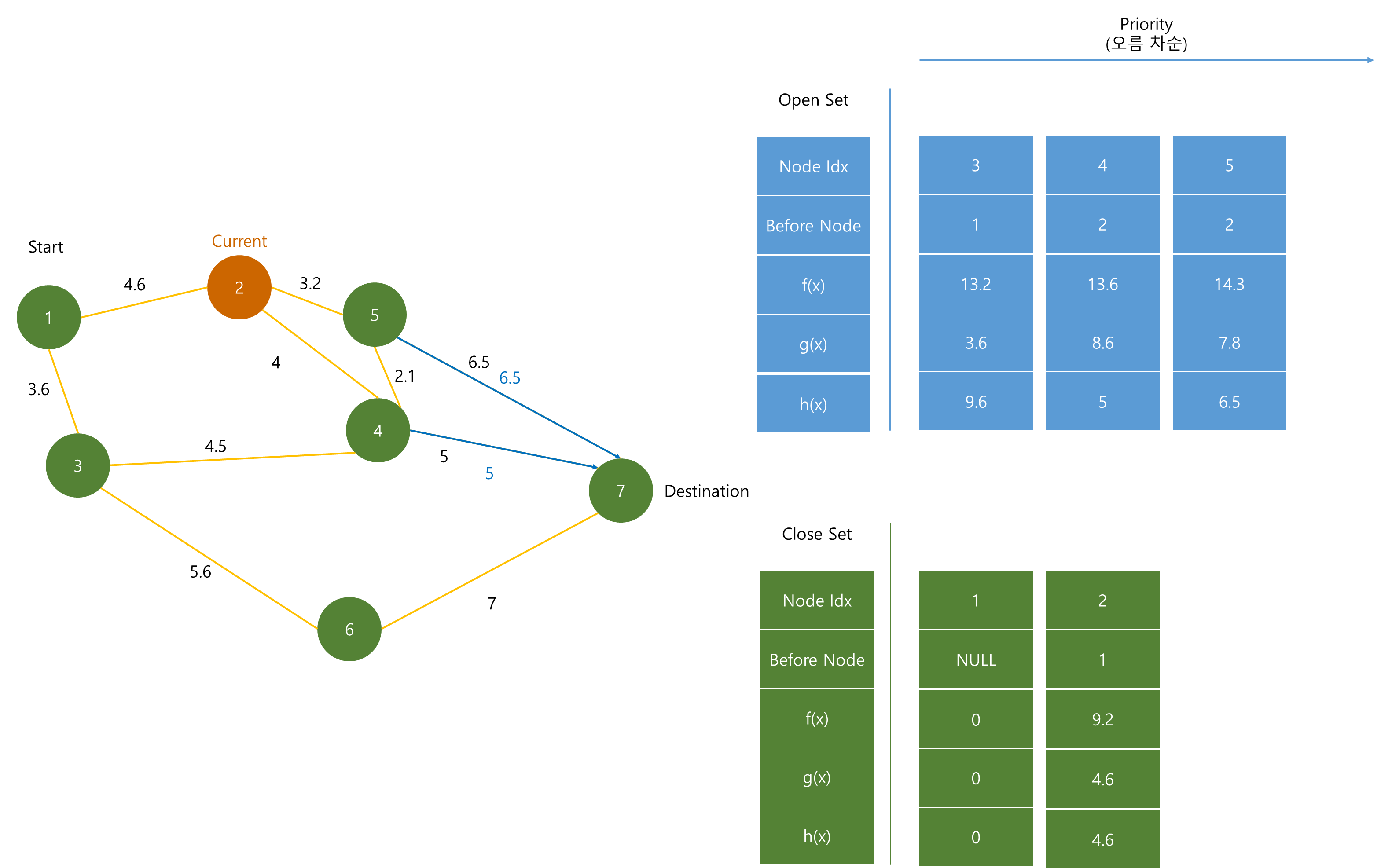
(2)와 이웃한 (4), (5) 노드의 dist를 수정하고 h(x)와 더한다. 이 때 (4), (5) 노드는 도착 노드와 연결되어 있으므로 실제 거리와 측정 값이 같다.
h(x)와 더한 값을 Priority Queue에 저장한다.
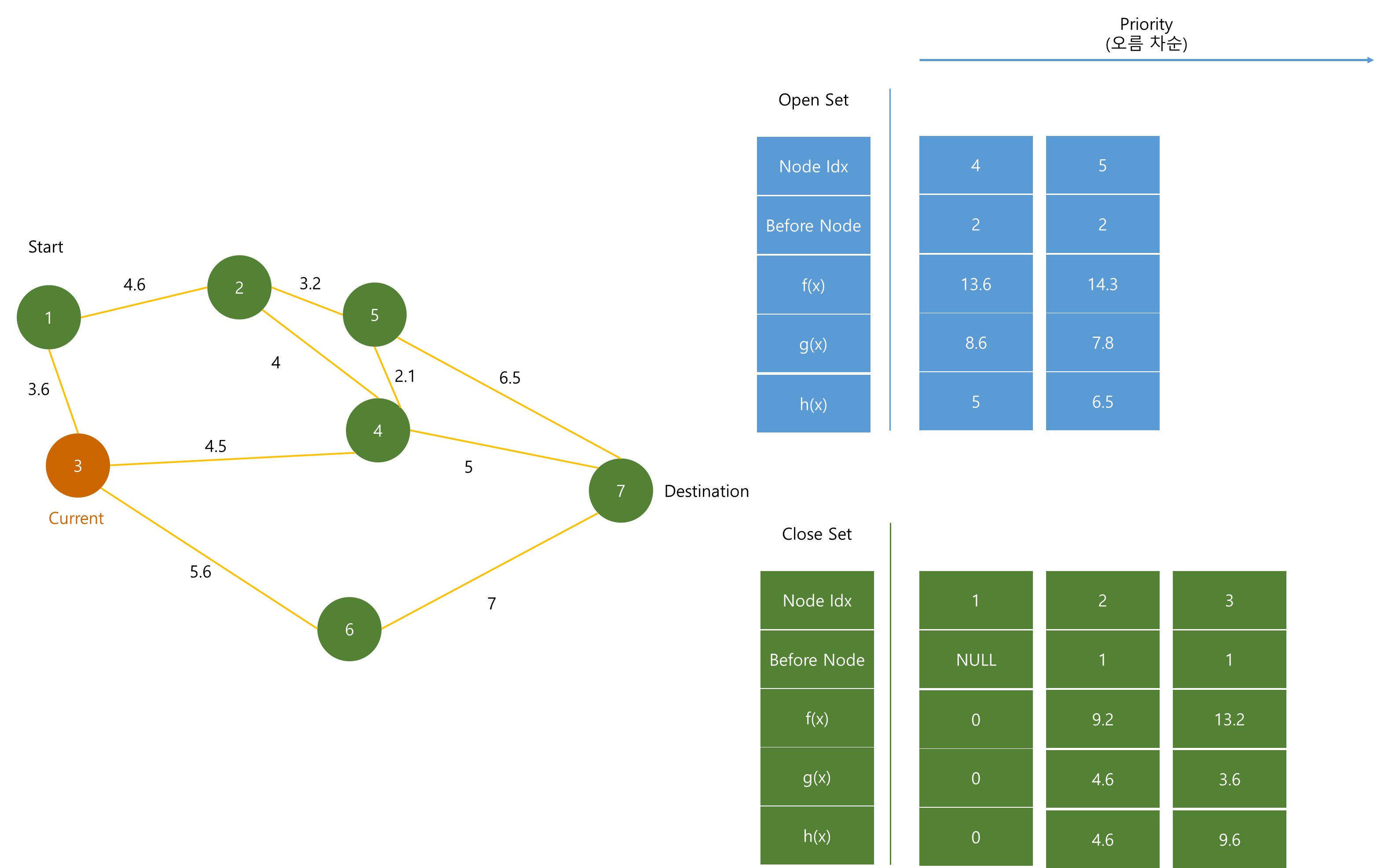
(5), (6)의 f(x) 값이, (1)에서 추가한 (3) 노드보다 크기 때문에 (3) 노드가 pop 된 후 Close Set에 저장된다.
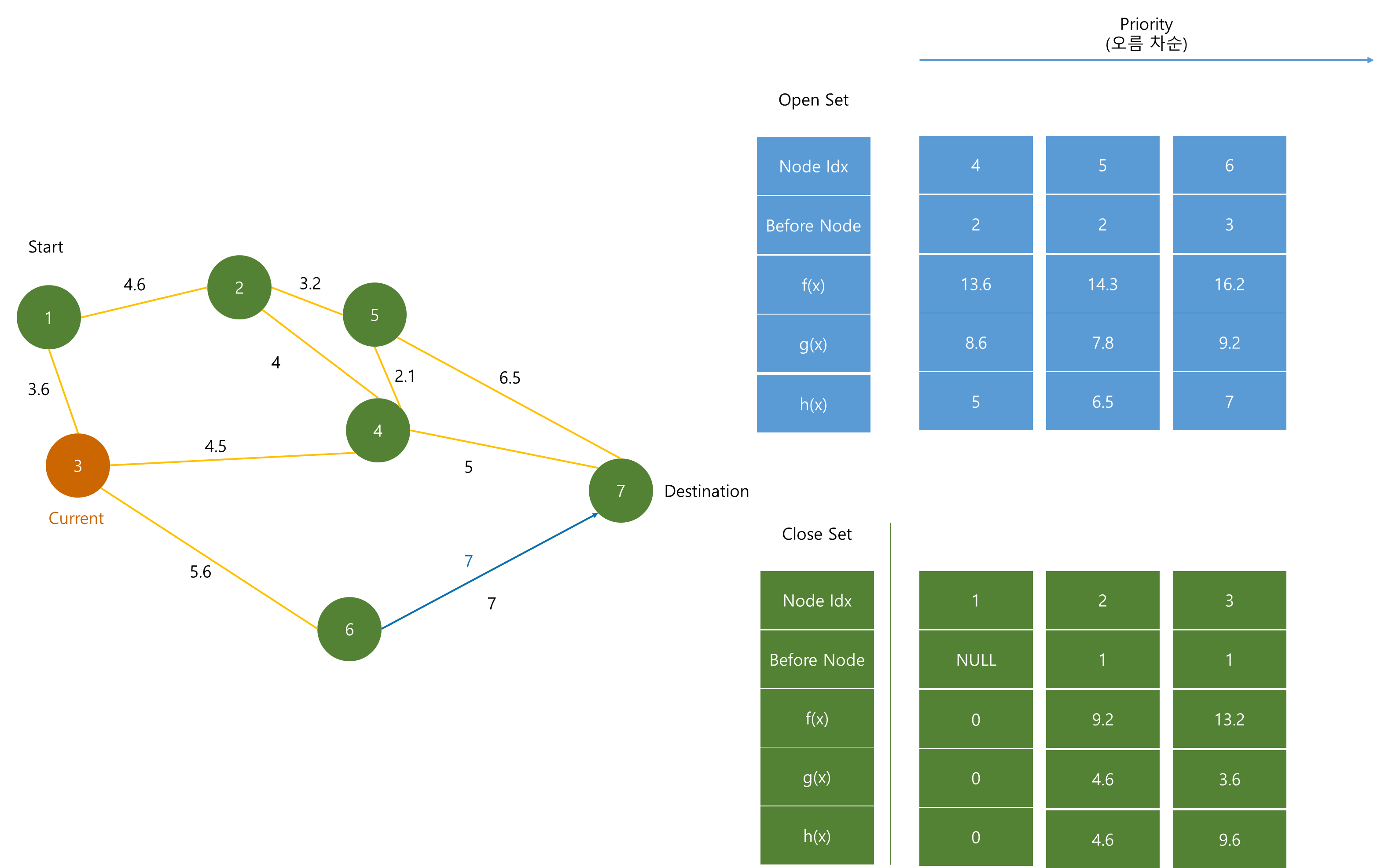
(3)은 (6) 노드와 연결되어 있으니 (6)의 dist를 수정하고 h(x)와 더한 후 Priority Queue에 저장한다.
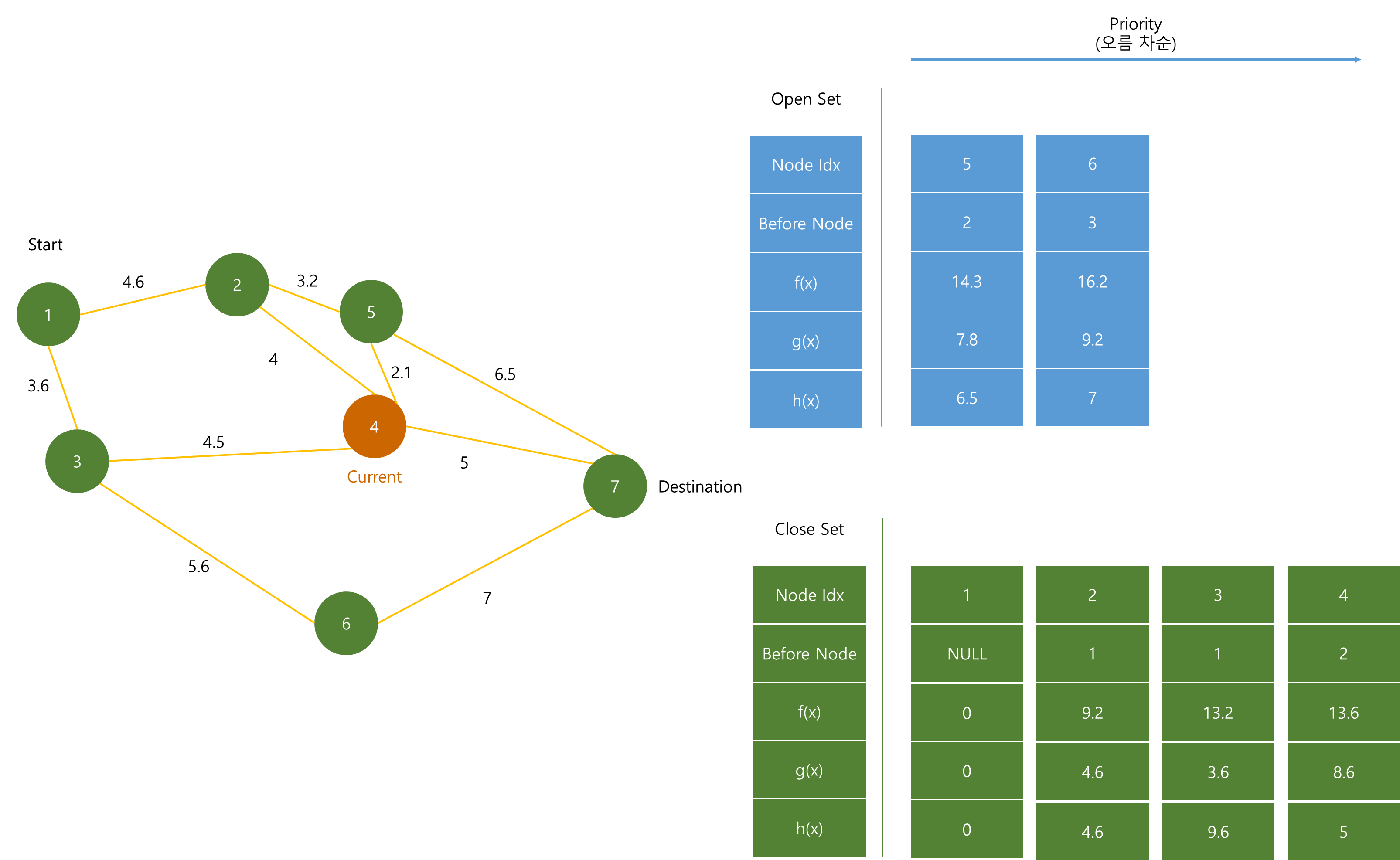
Priority Queue에서 가장 작은 f(x)인 (4) 노드가 pop 된 후 Close Set에 저장된다.
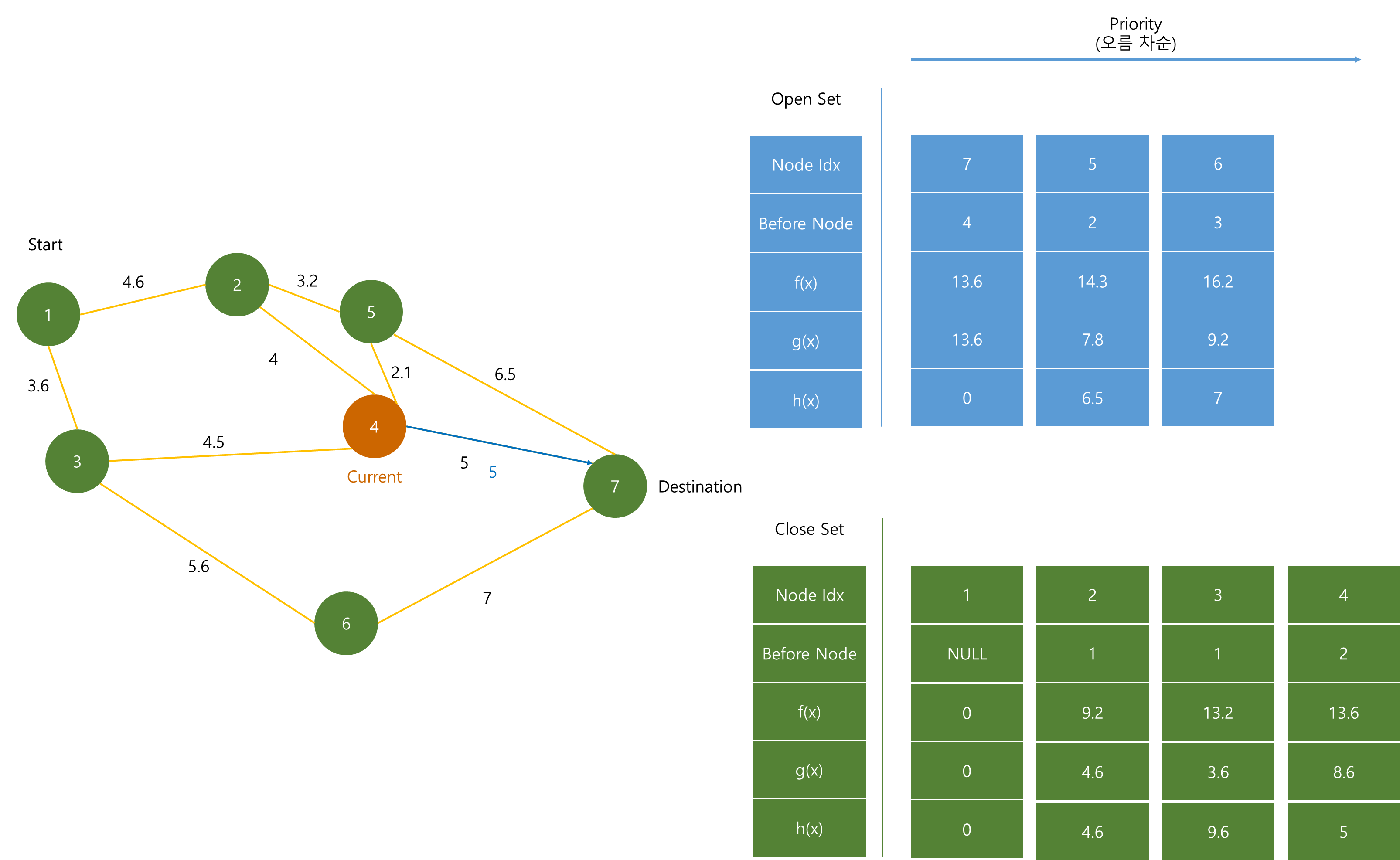
(4) 노드는 (5)와 (7) 노드에 연결되어 있다. 하지만 (5) 노드는 (1) - (2) - (4) - (5) 경로의 dist 값 보다 Priority Queue에 저장되어 있는 dist 값이 더 작으므로 이 때 (5)의 dist는 수정하지 않는다.
따라서 (7) 노드만 dist 값을 수정한 후 h(x) 값과 더해 Priority Queue에 추가한다.
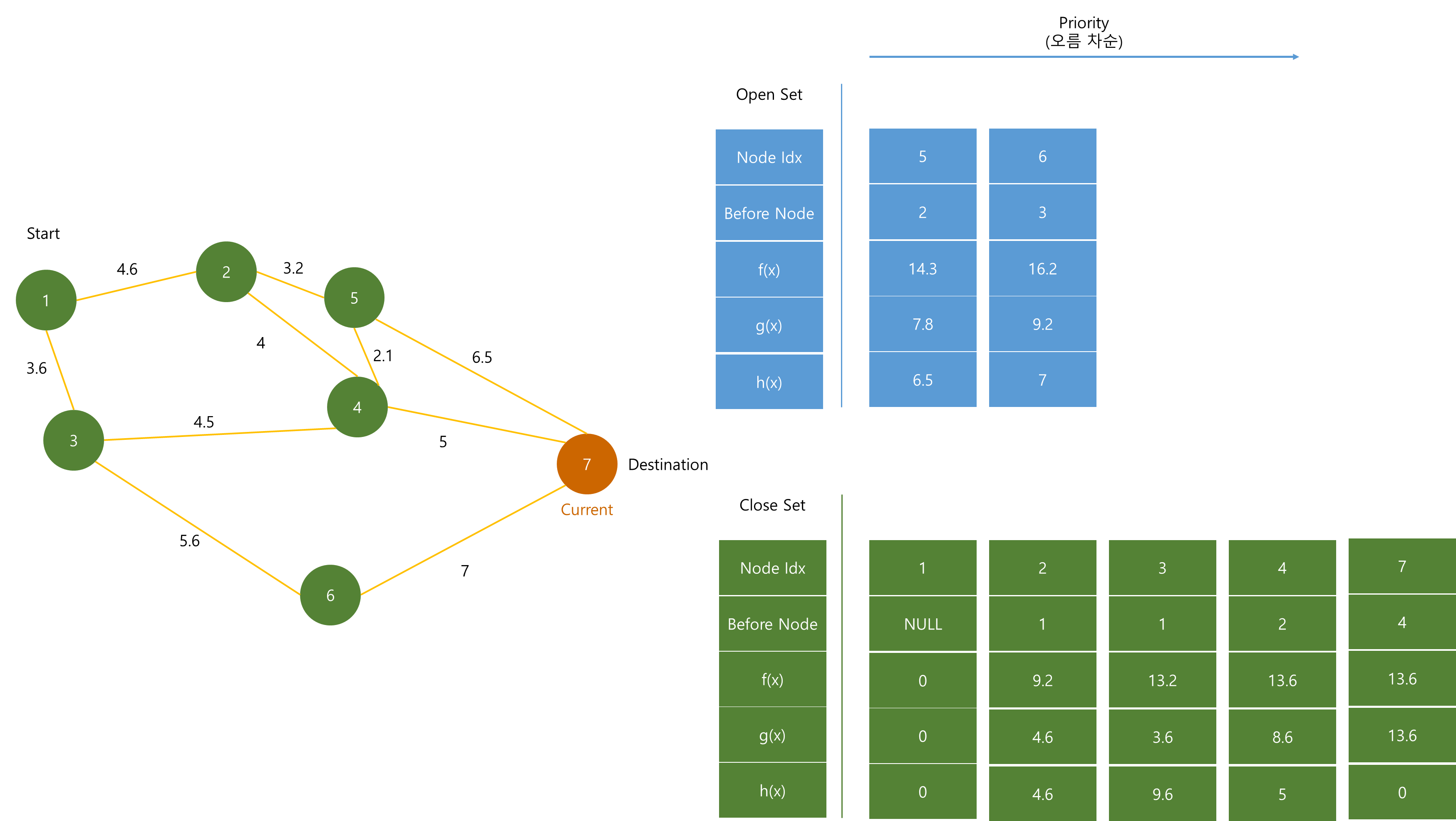
Priority Queue에서 가장 작은 f(x)인 (7)을 pop한다.
이 때 Destination Node와 (7)이 같으니 알고리즘을 종료한다.
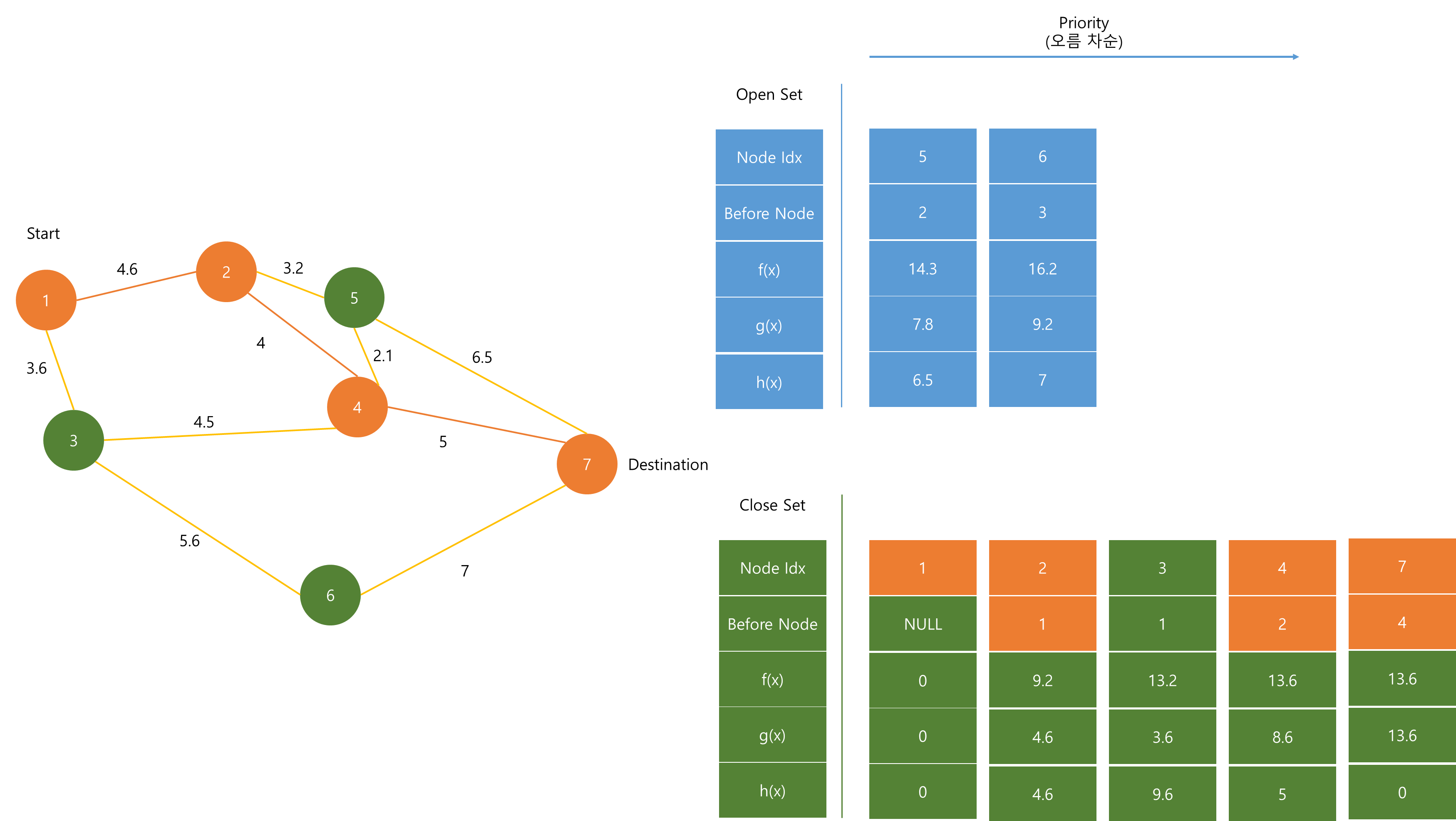
Path를 구성할 때는 Close Set의 정보를 이용해 Destination 노드부터 계속 이전 노드를 null이 나올 때까지 참조하면 최단 경로가 완성된다.
https://github.com/MunHwaDong/Algorithm/blob/master/graph/AStar.cs
Algorithm/graph/AStar.cs at master · MunHwaDong/Algorithm
Contribute to MunHwaDong/Algorithm development by creating an account on GitHub.
github.com
'CS > Unity' 카테고리의 다른 글
| [멋쟁이사자처럼 유니티 게임 개발 3기 TIL] Bubble Sort, Quick Sort (0) | 2024.12.12 |
|---|---|
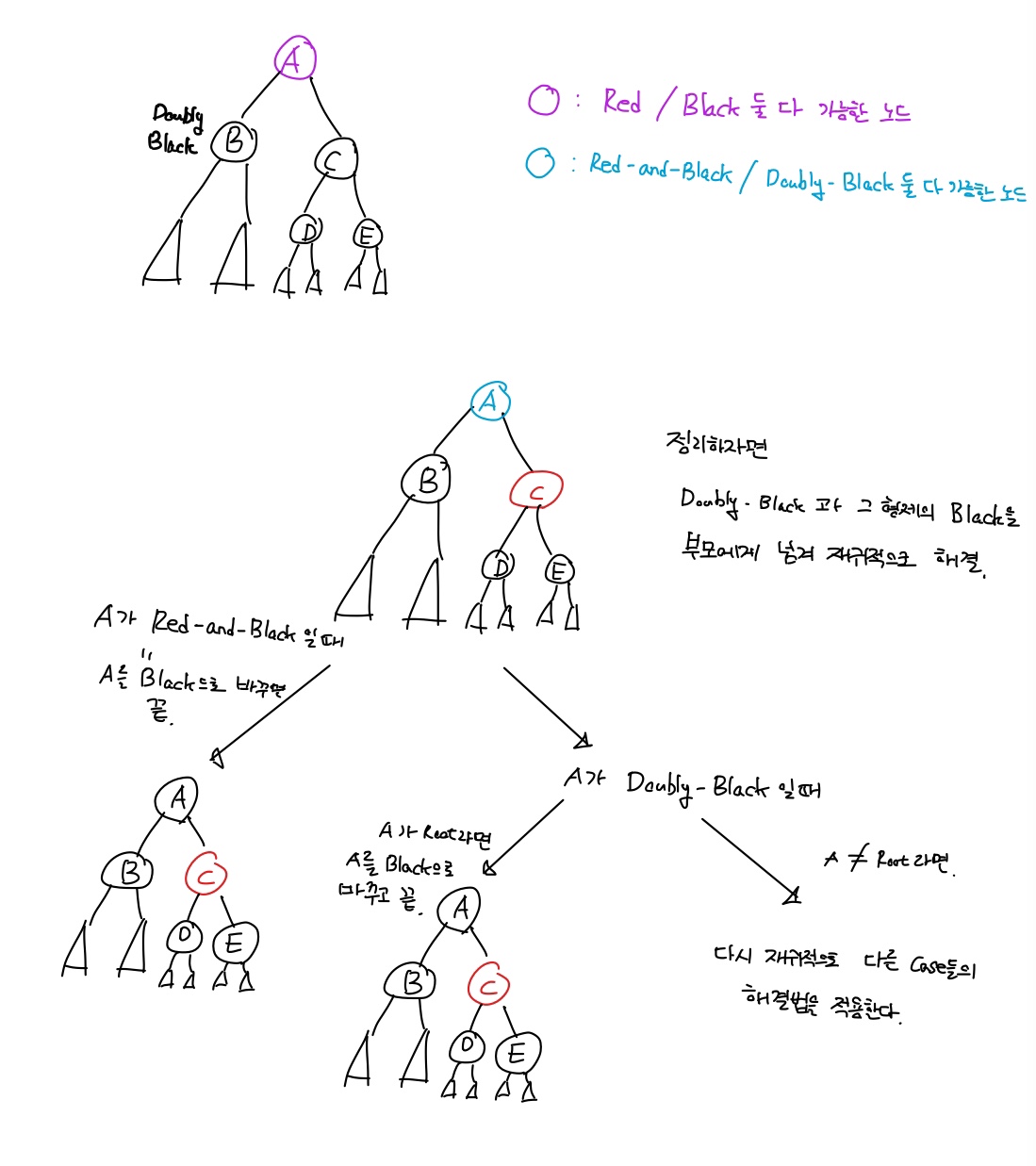
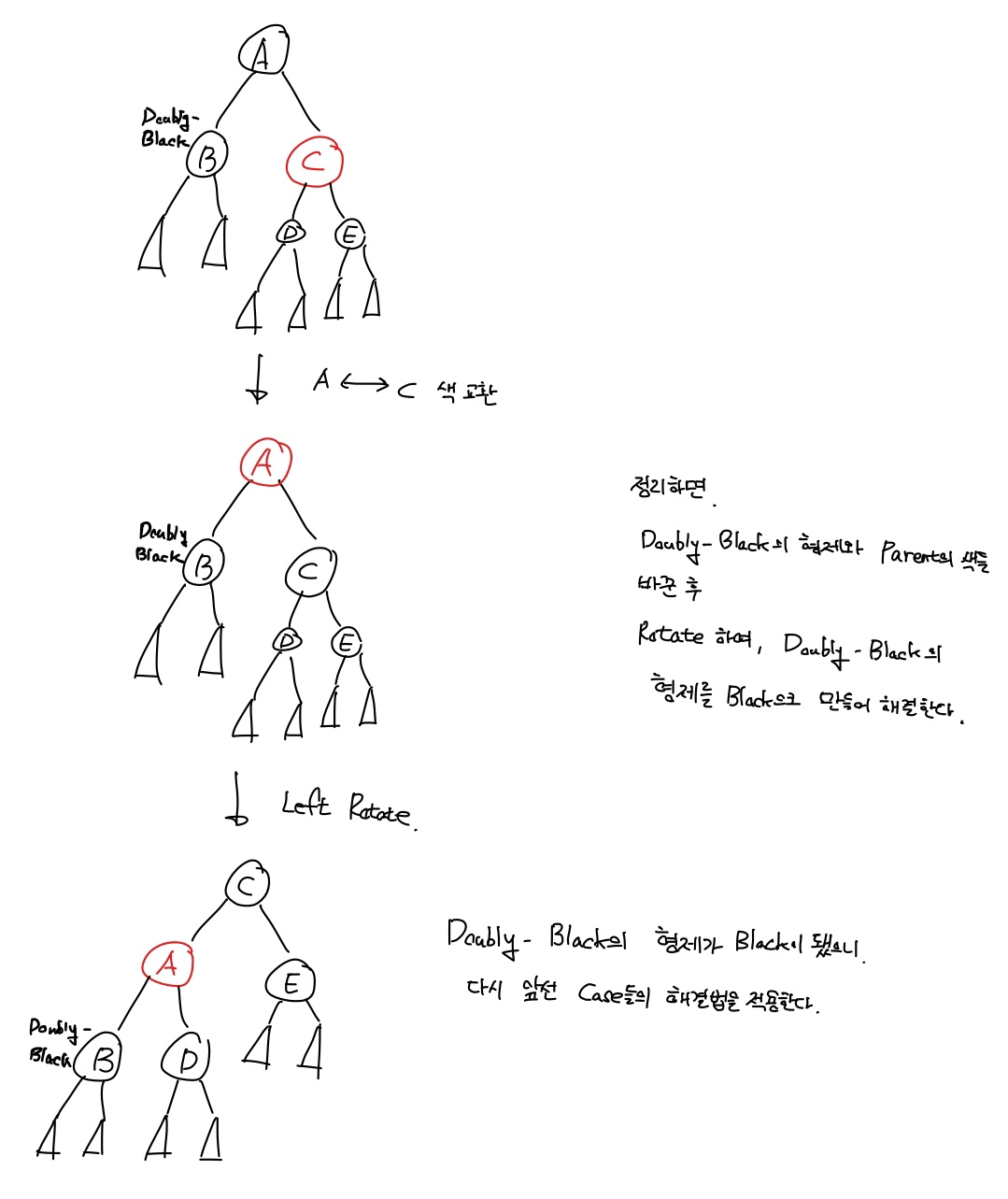
| [멋쟁이사자처럼 유니티 게임 개발 3기 TIL] Red Black Tree (0) | 2024.12.12 |
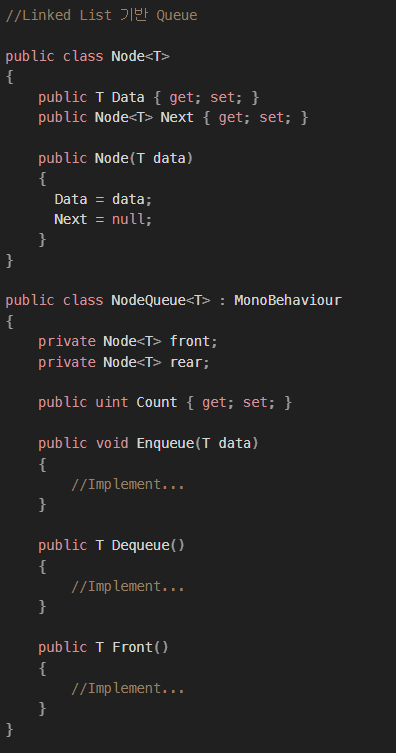
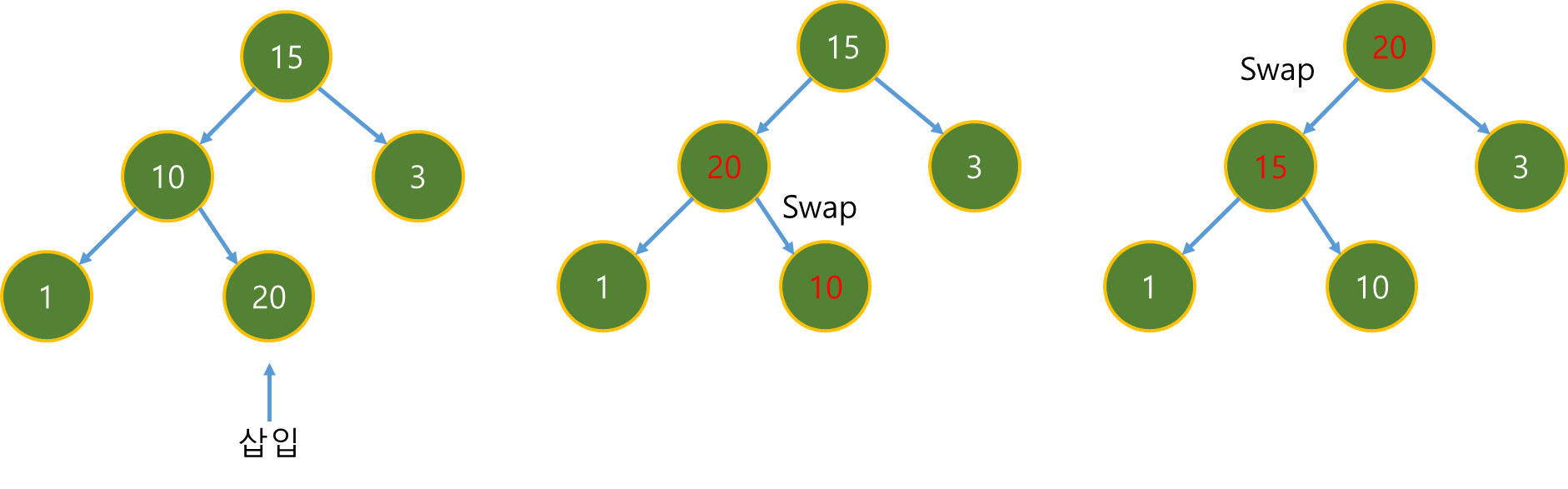
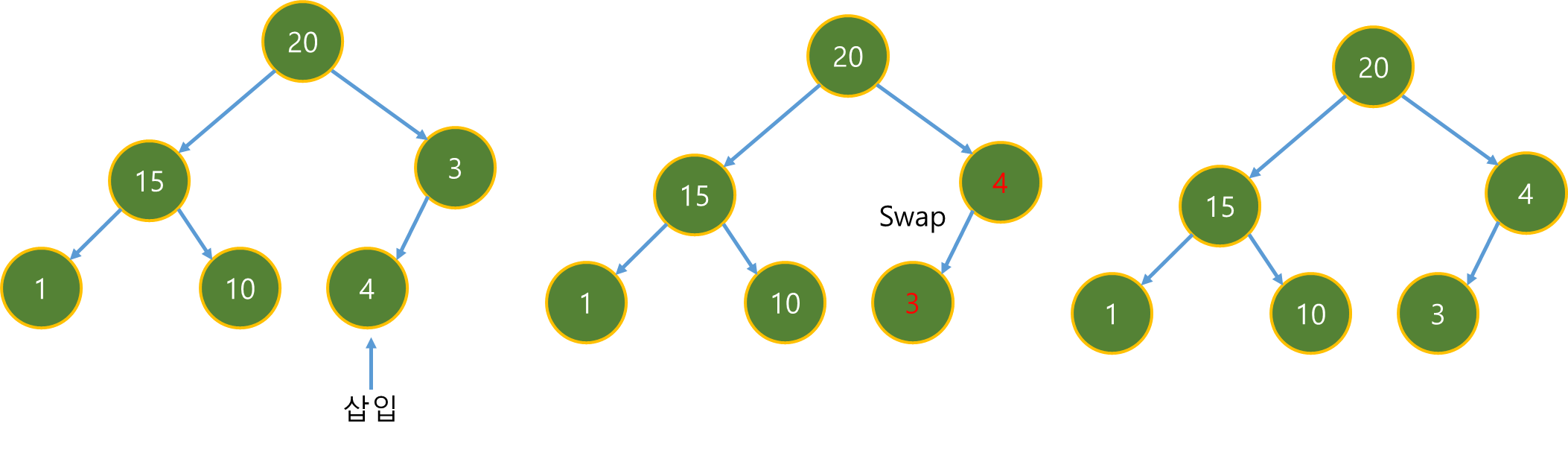
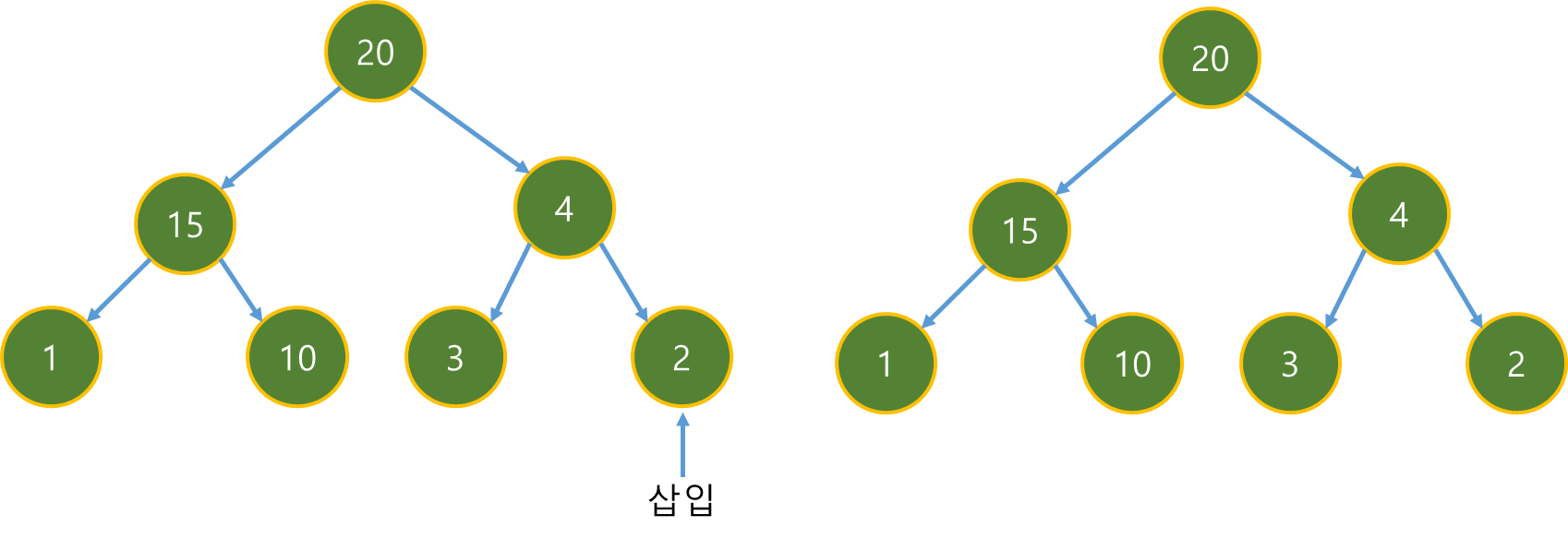
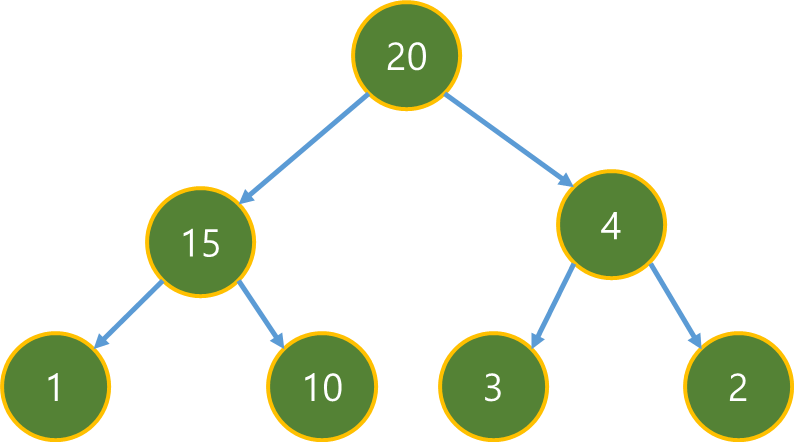
| [멋쟁이사자처럼 유니티 게임 개발 3기 TIL] Queue, Heap, Priority Queue (0) | 2024.12.07 |
| [멋쟁이사자처럼 유니티 게임 개발 3기 TIL] LINQ, Command Pattern (1) | 2024.12.05 |
| [멋쟁이사자처럼 유니티 게임 개발 3기 TIL] Stack, Custom Editor (0) | 2024.12.04 |